每天扫码支付、加好友、连WiFi,你有没有想过这黑白方块背后到底藏着什么猫腻?作为前端工程师,咱们不只要会用
qrcode.js这类第三方库,更要知道这玩意儿是怎么从一段字符串变成手机能认的图案的。
今天这篇文章,咱们就从0到1手撸一个二维码生成器,全程用原生JS实现,不依赖任何第三方库。放心,我会把每个技术点拆解得明明白白,保证你看完就能上手。准备好,咱们要开始钻牛角尖了!
一、二维码生成全景流程图
先上张全景图镇楼,咱们心里有个数,二维码是怎么一步步诞生的:
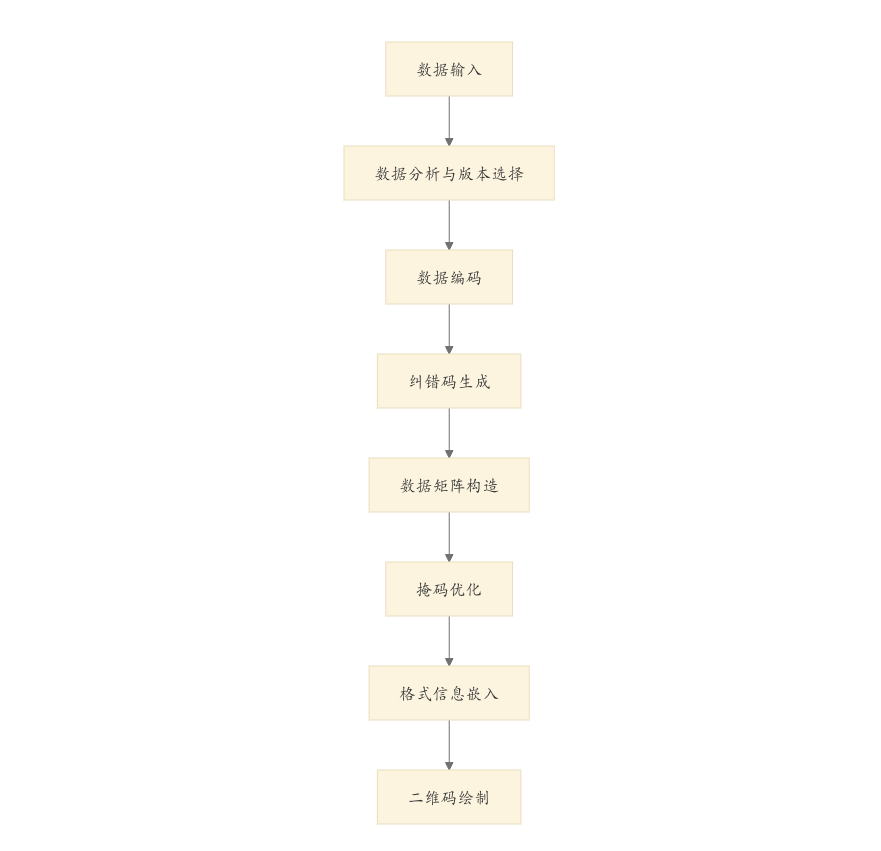
这七个步骤,就是把一段普通文本变成二维码图片的全过程。别看着复杂,咱们一个一个来啃,保证比你女朋友的心思还好懂。
二、核心技术拆解(附实战代码)
2.1 数据编码:把字符串变成二进制
咱们先思考个问题:二维码本质上就是一堆黑白方块,这些方块只认识0和1。所以第一步,就得把我们输入的文本(比如"hello world"或者网址)变成二进制的01串。
但这里有个门道:不同类型的数据,编码方式不一样,效率也差很多。二维码规定了四种编码模式:
数字模式:仅包含0-9,效率最高,3个数字用10位二进制表示 字母数字模式:包含0-9、A-Z(大写)、空格和一些符号,2个字符用11位表示 字节模式:可以表示任何ISO-8859-1字符,每个字符用8位表示 汉字模式:用于汉字,每个汉字用13位表示(注意:不是所有二维码扫描器都支持)
所以,智能的编码方式应该是:根据输入内容自动选择最合适的编码模式,并且在内容混杂时能自动切换模式。
2.1.1 编码模式自动识别
咱们先来实现一个函数,判断一段文本应该用什么编码模式:
/**
* 判断文本应该使用的最佳编码模式
* @param {string} text 输入文本
* @returns {string} 编码模式标识 ('numeric', 'alphanumeric', 'byte', 'kanji')
*/
function detectBestEncodingMode(text) {
// 检查是否全是数字
const numericRegex = /^[0-9]*$/;
if (numericRegex.test(text)) {
return 'numeric';
}
// 检查是否是字母数字模式(支持的字符集)
const alphanumericChars = '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ $%*+-./:';
const alphanumericRegex = new RegExp(`^[${alphanumericChars}]*$`);
if (alphanumericRegex.test(text)) {
return 'alphanumeric';
}
// 检查是否是纯ASCII字符(字节模式)
const asciiRegex = /^[\x00-\x7F]*$/;
if (asciiRegex.test(text)) {
return 'byte';
}
// 默认为字节模式(实际应用中可能需要判断汉字模式)
return 'byte';
}这个函数会按照"数字→字母数字→字节"的优先级来选择编码模式,因为越是靠前的模式,编码效率越高。比如同样是"123456",用数字模式编码只需要20位(每3个数字10位),而用字节模式则需要48位(每个数字8位)。
2.1.2 模式指示器与字符计数
确定了编码模式后,我们还需要告诉二维码扫描器两件事:
我们用的是什么编码模式 这个编码模式下有多少个字符
二维码标准为每种模式分配了一个"模式指示器":
数字模式:0001(4位) 字母数字模式:0010(4位) 字节模式:0100(4位) 汉字模式:1000(4位)
字符计数的位数则根据二维码的"版本"和编码模式而不同。二维码的版本从1到40,版本1是21x21的矩阵,每增加一个版本,矩阵 size 增加4个模块(宽高各+4),到版本40就是177x177的矩阵。
不同版本支持的字符计数位数:
| 版本范围 | 数字模式 | 字母数字模式 | 字节模式 | 汉字模式 |
|---|---|---|---|---|
| 1-9 | 10位 | 9位 | 8位 | 8位 |
| 10-26 | 12位 | 11位 | 16位 | 10位 |
| 27-40 | 14位 | 13位 | 16位 | 12位 |
所以,我们需要一个函数来获取字符计数字段的长度:
/**
* 获取字符计数字段的位数
* @param {number} version 二维码版本(1-40)
* @param {string} mode 编码模式
* @returns {number} 字符计数字段的位数
*/
function getCharCountIndicatorLength(version, mode) {
if (version >= 1 && version <= 9) {
const lengths = { 'numeric': 10, 'alphanumeric': 9, 'byte': 8, 'kanji': 8 };
return lengths[mode];
} else if (version >= 10 && version <= 26) {
const lengths = { 'numeric': 12, 'alphanumeric': 11, 'byte': 16, 'kanji': 10 };
return lengths[mode];
} else { // 27-40
const lengths = { 'numeric': 14, 'alphanumeric': 13, 'byte': 16, 'kanji': 12 };
return lengths[mode];
}
}2.1.3 三种编码模式的具体实现
现在,咱们来实现三种主要编码模式的核心算法:
数字模式编码:
数字模式的编码规则很简单:每3个数字一组,转成10位二进制。如果剩下1个数字,转成4位;剩下2个数字,转成7位。
/**
* 数字模式编码
* @param {string} data 仅包含数字的字符串
* @returns {string} 编码后的二进制字符串
*/
function encodeNumeric(data) {
let bits = '';
// 每3个数字一组处理
for (let i = 0; i < data.length; i += 3) {
// 取3个数字,不足3个则取剩下的
const group = data.substr(i, 3);
// 转成数字
const num = parseInt(group, 10);
let bitLength;
if (group.length === 1) {
bitLength = 4; // 1个数字 -> 4位
} else if (group.length === 2) {
bitLength = 7; // 2个数字 -> 7位
} else {
bitLength = 10; // 3个数字 -> 10位
}
// 转成二进制并填充前导零至指定长度
let binary = num.toString(2);
while (binary.length < bitLength) {
binary = '0' + binary;
}
bits += binary;
}
return bits;
}字母数字模式编码:
字母数字模式包含45个字符,每个字符都有对应的索引值(见下表)。编码时每2个字符一组,第一个字符的索引乘以45再加上第二个字符的索引,结果转成11位二进制。如果剩下1个字符,直接转成6位二进制。
字母数字字符集及索引:
0:0, 1:1, ..., 9:9, 10:A, 11:B, ..., 35:Z, 36:空格, 37:$, 38:%, 39:*, 40:+, 41:-, 42:., 43:/, 44::
/**
* 字母数字模式编码
* @param {string} data 字母数字字符串
* @returns {string} 编码后的二进制字符串
*/
function encodeAlphanumeric(data) {
// 字符到索引的映射表
const charMap = '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ $%*+-./:';
let bits = '';
// 每2个字符一组处理
for (let i = 0; i < data.length; i += 2) {
// 取当前字符和下一个字符(如果存在)
const c1 = data[i];
const c2 = i + 1 < data.length ? data[i + 1] : null;
if (c2) {
// 两个字符:索引 = c1索引 * 45 + c2索引,转成11位二进制
const index1 = charMap.indexOf(c1);
const index2 = charMap.indexOf(c2);
const combined = index1 * 45 + index2;
let binary = combined.toString(2);
// 确保是11位,不足则补前导零
while (binary.length < 11) {
binary = '0' + binary;
}
bits += binary;
} else {
// 单个字符:直接转成6位二进制
const index = charMap.indexOf(c1);
let binary = index.toString(2);
while (binary.length < 6) {
binary = '0' + binary;
}
bits += binary;
}
}
return bits;
}字节模式编码:
字节模式相对简单,就是把每个字符转成其ISO-8859-1编码值(0-255),再转成8位二进制。对于中文等非ISO-8859-1字符,通常会先转成UTF-8字节序列,再进行编码。
/**
* 字节模式编码
* @param {string} data 字符串
* @returns {string} 编码后的二进制字符串
*/
function encodeByte(data) {
let bits = '';
// 将字符串转换为UTF-8字节数组
const encoder = new TextEncoder('utf-8');
const bytes = encoder.encode(data);
// 每个字节转成8位二进制
for (const byte of bytes) {
let binary = byte.toString(2);
// 确保是8位,不足则补前导零
while (binary.length < 8) {
binary = '0' + binary;
}
bits += binary;
}
return bits;
}2.1.4 数据编码总函数
现在我们可以把上面的函数整合起来,实现一个完整的数据编码流程:
/**
* 数据编码主函数
* @param {string} text 输入文本
* @param {number} version 二维码版本
* @returns {string} 完整的编码后二进制字符串
*/
function encodeData(text, version) {
// 1. 检测最佳编码模式
const mode = detectBestEncodingMode(text);
console.log(`检测到最佳编码模式: ${mode}`);
// 2. 获取模式指示器
const modeIndicators = {
'numeric': '0001',
'alphanumeric': '0010',
'byte': '0100',
'kanji': '1000'
};
const modeIndicator = modeIndicators[mode];
// 3. 计算字符计数指示符
const charCount = text.length;
const charCountLength = getCharCountIndicatorLength(version, mode);
let charCountBinary = charCount.toString(2);
// 补前导零至指定长度
while (charCountBinary.length < charCountLength) {
charCountBinary = '0' + charCountBinary;
}
// 4. 根据模式编码数据
let dataBits = '';
switch (mode) {
case 'numeric':
dataBits = encodeNumeric(text);
break;
case 'alphanumeric':
dataBits = encodeAlphanumeric(text);
break;
case 'byte':
dataBits = encodeByte(text);
break;
case 'kanji':
// 汉字模式实现略,原理类似
dataBits = '';
break;
}
// 5. 连接所有部分:模式指示器 + 字符计数 + 数据位
let encodedData = modeIndicator + charCountBinary + dataBits;
// 6. 添加终止符:最多4个0,直到数据长度达到当前版本的码字总数的8倍
const totalCodewords = getTotalCodewords(version); // 这个函数我们后面会实现
const requiredBits = totalCodewords * 8;
// 计算需要添加的终止符长度
let terminatorLength = Math.min(4, requiredBits - encodedData.length);
encodedData += '0'.repeat(terminatorLength);
// 7. 如果还没达到需要的长度,用补齐符填充(8位一组的11101100和00010001)
if (encodedData.length % 8 !== 0) {
const padLength = 8 - (encodedData.length % 8);
encodedData += '0'.repeat(padLength);
}
// 8. 如果仍然不够,用填充码字填充
const padCodewords = ['11101100', '00010001'];
let padIndex = 0;
while (encodedData.length < requiredBits) {
encodedData += padCodewords[padIndex];
padIndex = (padIndex + 1) % 2; // 交替使用两个填充码字
}
return encodedData;
}到这里,我们已经把原始文本转换成了二维码能理解的二进制数据流。这一步就像是把我们想说的话翻译成二维码的"母语",是整个生成过程的基础。
2.2 纠错引擎:Reed-Solomon编码实战
现在我们有了编码后的数据,但只有数据还不够。二维码之所以靠谱,很大程度上是因为它强大的纠错能力——就算被挡住一部分、有点污损,照样能扫出来。
这个纠错能力是怎么来的?靠的就是 Reed-Solomon码(里德-所罗门码),一种强大的纠错编码技术。CD、DVD、蓝光光盘、卫星通信中都用它来纠错。
2.2.1 Reed-Solomon码的基本原理
Reed-Solomon码(简称RS码)是一种前向纠错码,它的核心思想是:在原始数据后面添加一些校验码(纠错码),使得即使部分数据丢失或出错,也能通过这些校验码恢复出原始数据。
二维码中使用的是 RS(n, k) 码,其中:
n 是码字总数(数据码 + 纠错码) k 是数据码数量 纠错码数量 = n - k 最多能纠正 t = (n - k)/2 个错误码字
二维码定义了四个纠错级别:
L级(低):7%的码字可以被纠正 M级(中):15%的码字可以被纠正 Q级(较高):25%的码字可以被纠正 H级(高):30%的码字可以被纠正
不同版本、不同纠错级别的二维码,其数据码和纠错码的数量都有明确规定。比如版本1、L级纠错的二维码有16个数据码,7个纠错码,构成RS(23, 16)码,最多能纠正3个错误码字。
2.2.2 伽罗瓦域(GF(2^8))运算
RS码的所有运算都在伽罗瓦域(有限域)中进行,二维码使用的是GF(2^8)域(包含256个元素)。这部分是整个二维码生成中最复杂的数学部分,咱们得慢慢啃。
首先,我们需要构建GF(2^8)域的元素表和运算表。在GF(2^8)中,每个元素可以表示为一个8位二进制数(0-255)。加法就是按位异或(XOR),乘法则比较复杂,需要使用不可约多项式。二维码标准规定使用的不可约多项式是:x⁸ + x⁴ + x³ + x² + 1(十六进制0x11D)。
伽罗瓦域乘法实现:
/**
* GF(2^8)域乘法
* @param {number} a 乘数a (0-255)
* @param {number} b 乘数b (0-255)
* @returns {number} 乘积 (0-255)
*/
function gfMultiply(a, b) {
if (a === 0 || b === 0) return 0;
let result = 0;
// 不可约多项式: x⁸ + x⁴ + x³ + x² + 1 = 0x11D
const irreducible = 0x11D;
for (let i = 0; i < 8; i++) {
// 如果b的第i位是1
if ((b & (1 << i)) !== 0) {
// 左移i位相当于乘以α^i
let aShifted = a << i;
// 模不可约多项式,确保结果是8位
for (let j = 7 + i; j >= 8; j--) {
if ((aShifted & (1 << j)) !== 0) {
aShifted ^= irreducible << (j - 8);
}
}
result ^= aShifted;
}
}
// 取低8位作为结果
return result & 0xFF;
}为了提高效率,实际应用中我们会预先生成一个乘法表,而不是每次都实时计算:
// 预生成GF(2^8)乘法表
const gfMulTable = new Array(256);
for (let i = 0; i < 256; i++) {
gfMulTable[i] = new Array(256);
for (let j = 0; j < 256; j++) {
gfMulTable[i][j] = gfMultiply(i, j);
}
}2.2.3 生成多项式
RS码的纠错码是通过将数据多项式除以一个生成多项式得到的余式。生成多项式的形式为:
G(x) = (x - α^0)(x - α^1)...(x - α^(2t-1))
其中t是可纠正的错误数,α是GF(2^8)域的本原元。二维码中使用α = 2(即多项式x)。
对于纠错码数量为2t的RS码,生成多项式有2t个根。我们需要预先生成这些生成多项式的系数。
/**
* 生成Reed-Solomon生成多项式
* @param {number} degree 多项式次数(纠错码数量)
* @returns {number[]} 生成多项式系数数组
*/
function generateGeneratorPoly(degree) {
// 初始多项式为1 (x^0)
let poly = [1];
// 生成 (x - α^0)(x - α^1)...(x - α^(degree-1))
for (let i = 0; i < degree; i++) {
// 当前因子: (x - α^i),在GF(2^8)中表示为 [1, α^i]
const factor = [1, alphaPower(i)]; // alphaPower函数见下文
// 多项式乘法:poly = poly * factor
const newPoly = new Array(poly.length + factor.length - 1).fill(0);
for (let j = 0; j < poly.length; j++) {
for (let k = 0; k < factor.length; k++) {
newPoly[j + k] ^= gfMulTable[poly[j]][factor[k]];
}
}
poly = newPoly;
}
return poly;
}
/**
* 计算α^exp mod 不可约多项式
* @param {number} exp 指数
* @returns {number} α^exp在GF(2^8)中的值
*/
function alphaPower(exp) {
if (exp === 0) return 1;
let result = 1; // α^0 = 1
for (let i = 0; i < exp; i++) {
result = gfMulTable[result][2]; // α^(i+1) = α^i * α,而α=2
if (result >= 256) {
result ^= 0x11D; // 模不可约多项式
}
}
return result;
}2.2.4 多项式除法与纠错码计算
有了生成多项式,我们就可以通过多项式除法来计算纠错码了。具体步骤是:
将数据码视为一个多项式D(x) 在D(x)后面添加2t个0(纠错码数量),得到x^(2t)D(x) 用生成多项式G(x)除x^(2t)D(x),得到商式Q(x)和余式R(x),满足x^(2t)D(x) = Q(x)G(x) + R(x) 纠错码就是余式R(x)的系数(取反后,因为在GF(2)中减法等于加法)
/**
* 计算Reed-Solomon纠错码
* @param {number[]} data 数据码数组
* @param {number}纠错码数量
* @returns {number[]} 纠错码数组
*/
function rsEncode(data,纠错码数量) {
// 1. 生成生成多项式
const genPoly = generateGeneratorPoly(纠错码数量);
// 2. 初始化被除数:数据码 + 纠错码数量个0
const dividend = [...data, ...new Array(纠错码数量).fill(0)];
// 3. 多项式除法
for (let i = 0; i < data.length; i++) {
const coef = dividend[i];
if (coef !== 0) {
for (let j = 0; j < genPoly.length; j++) {
dividend[i + j] ^= gfMulTable[coef][genPoly[j]];
}
}
}
// 4. 余数就是纠错码(取最后纠错码数量个元素)
const纠错码 = dividend.slice(data.length);
return纠错码;
}2.2.5 数据分块与交织
对于较高版本的二维码,数据和纠错码会被分成多个块,每个块独立进行RS编码,然后再交织排列。这样做的好处是,即使二维码的某一整行或整列被损坏,也只会影响每个块中的一小部分,而不是整个块。
分块规则比较复杂,不同版本、不同纠错级别的分块方式都不同。我们需要一个函数来获取特定版本和纠错级别的分块信息:
/**
* 获取二维码分块信息
* @param {number} version 版本
* @param {string} errorCorrectionLevel 纠错级别('L', 'M', 'Q', 'H')
* @returns {Object} 分块信息
*/
function getQRCodeBlocks(version, errorCorrectionLevel) {
// 这里简化处理,实际应该根据二维码标准返回分块信息
// 完整版需要包含每个块的数据码数量、纠错码数量等信息
// 可参考二维码规范中的"错误修正级别和掩模图案参考表"
// 以版本1、L级纠错为例:1个块,16个数据码,7个纠错码
if (version === 1 && errorCorrectionLevel === 'L') {
return {
count: 1, // 块数量
blocks: [
{ dataCodeCount: 16,纠错码数量: 7 }
]
};
}
// 其他版本和纠错级别的分块信息省略...
return { count: 1, blocks: [{ dataCodeCount: 16,纠错码数量: 7 }] };
}有了分块信息,我们就可以进行分块编码和交织了:
/**
* 数据分块、纠错编码与交织
* @param {string} encodedDataBits 编码后的二进制字符串
* @param {number} version 版本
* @param {string} errorCorrectionLevel 纠错级别
* @returns {number[]} 交织后的码字数组
*/
function processErrorCorrection(encodedDataBits, version, errorCorrectionLevel) {
// 1. 将二进制字符串转换为字节数组(码字)
const dataCodewords = [];
for (let i = 0; i < encodedDataBits.length; i += 8) {
const byte = encodedDataBits.substr(i, 8);
dataCodewords.push(parseInt(byte, 2));
}
// 2. 获取分块信息
const blockInfo = getQRCodeBlocks(version, errorCorrectionLevel);
const totalDataCodewords = blockInfo.blocks.reduce((sum, block) => sum + block.dataCodeCount, 0);
// 3. 检查数据码数量是否匹配
if (dataCodewords.length !== totalDataCodewords) {
throw new Error(`数据码数量不匹配: 实际${dataCodewords.length}, 需要${totalDataCodewords}`);
}
// 4. 分块并计算每个块的纠错码
const blocks = [];
let dataIndex = 0;
for (const block of blockInfo.blocks) {
// 提取当前块的数据码
const blockData = dataCodewords.slice(dataIndex, dataIndex + block.dataCodeCount);
dataIndex += block.dataCodeCount;
// 计算当前块的纠错码
const纠错码 = rsEncode(blockData, block.纠错码数量);
// 保存块数据和纠错码
blocks.push({ data: blockData,纠错码:纠错码 });
}
// 5. 交织:按列读取所有块的数据和纠错码
const interleaved = [];
const maxDataLength = Math.max(...blocks.map(b => b.data.length));
const max纠错码Length = Math.max(...blocks.map(b => b.纠错码.length));
// 先交织数据码
for (let i = 0; i < maxDataLength; i++) {
for (const block of blocks) {
if (i < block.data.length) {
interleaved.push(block.data[i]);
}
}
}
// 再交织纠错码
for (let i = 0; i < max纠错码Length; i++) {
for (const block of blocks) {
if (i < block.纠错码.length) {
interleaved.push(block.纠错码[i]);
}
}
}
return interleaved;
}到这里,我们已经完成了纠错码的生成和数据交织。这一步是二维码可靠性的保障,也是整个生成过程中数学最密集的部分。如果你能理解RS编码的原理,那你已经超越了99%的前端工程师了!
2.3 矩阵构造:数据排布的艺术
现在我们有了经过编码和纠错处理的数据流,下一步就是把这些数据放到二维码矩阵的正确位置上。这可不是简单地从左到右、从上到下填进去,二维码里有很多特殊区域,数据只能放在特定的位置。
2.3.1 二维码的固定图案
先来认识一下二维码里的几个"特殊区域":
定位图案(Position Detection Patterns):就是二维码三个角上的大方块,用于确定二维码的位置和方向。每个定位图案都是7x7的正方形。
定时图案(Timing Patterns):两条贯穿矩阵的黑白相间的直线,用于确定模块的大小和位置。位于定位图案之间,宽度为1个模块。
对齐图案(Alignment Patterns):二维码中除了定位图案外的那些小方块,用于纠正畸变。不同版本的二维码有不同数量和位置的对齐图案。
格式信息(Format Information):存储纠错级别和掩码图案信息,位于定位图案旁边,共30位。
版本信息(Version Information):对于7以上的版本,会包含版本信息,位于矩阵的右下角和左上角,共18位。
这些特殊区域是不能放置数据的,我们需要先在矩阵中标出这些区域。
2.3.2 矩阵初始化与特殊区域绘制
首先,我们需要创建一个指定大小的矩阵(版本1是21x21,版本2是25x25,以此类推),然后在矩阵上绘制这些特殊区域。
/**
* 创建二维码矩阵并绘制固定图案
* @param {number} version 版本
* @returns {number[][]} 初始化后的矩阵,0=白色,1=黑色,-1=待填充数据
*/
function createQRMatrix(version) {
// 计算矩阵大小:size = 21 + 4*(version-1)
const size = 21 + 4 * (version - 1);
// 初始化矩阵:-1表示待填充数据,0表示白色,1表示黑色
const matrix = Array.from({ length: size }, () => Array(size).fill(-1));
// 1. 绘制定位图案(三个角上的7x7方块)
drawPositionDetectionPatterns(matrix, size);
// 2. 绘制定时图案(定位图案之间的黑白线)
drawTimingPatterns(matrix, size);
// 3. 绘制对齐图案(根据版本确定位置)
drawAlignmentPatterns(matrix, size, version);
// 4. 绘制版本信息(版本7及以上)
if (version >= 7) {
drawVersionInformation(matrix, size, version);
}
return matrix;
}
/**
* 绘制定位图案
*/
function drawPositionDetectionPatterns(matrix, size) {
// 定位图案位置:左上角、右上角、左下角
const positions = [
{ x: 0, y: 0 }, // 左上角
{ x: size - 7, y: 0 }, // 右上角
{ x: 0, y: size - 7 } // 左下角
];
for (const pos of positions) {
const { x, y } = pos;
// 最外层黑色边框(7x7)
for (let i = 0; i < 7; i++) {
for (let j = 0; j < 7; j++) {
// 第一层和第六层(0-based)是黑色边框
if (i === 0 || i === 6 || j === 0 || j === 6) {
matrix[y + i][x + j] = 1;
}
// 第二层和第五层是白色边框
else if (i === 1 || i === 5 || j === 1 || j === 5) {
matrix[y + i][x + j] = 0;
}
// 中间3x3是黑色
else {
matrix[y + i][x + j] = 1;
}
}
}
}
}
/**
* 绘制定时图案
*/
function drawTimingPatterns(matrix, size) {
// 横向定时图案:位于左上角定位图案右侧,y=6,x从7到size-8
for (let x = 7; x < size - 7; x++) {
// 每隔一个模块交替黑白(从黑色开始)
matrix[6][x] = (x % 2 === 0) ? 1 : 0;
}
// 纵向定时图案:位于左上角定位图案下方,x=6,y从7到size-8
for (let y = 7; y < size - 7; y++) {
// 每隔一个模块交替黑白(从黑色开始)
matrix[y][6] = (y % 2 === 0) ? 1 : 0;
}
}
/**
* 绘制对齐图案
*/
function drawAlignmentPatterns(matrix, size, version) {
// 获取对齐图案位置(不同版本位置不同)
const alignmentPositions = getAlignmentPatternPositions(version);
for (const x of alignmentPositions) {
for (const y of alignmentPositions) {
// 跳过定位图案所在的位置
if ((x <= 6 && y <= 6) ||
(x >= size - 7 && y <= 6) ||
(x <= 6 && y >= size - 7)) {
continue;
}
// 绘制5x5的对齐图案
for (let i = -2; i <= 2; i++) {
for (let j = -2; j <= 2; j++) {
const distance = Math.max(Math.abs(i), Math.abs(j));
if (distance === 2) {
// 最外层:黑色
matrix[y + i][x + j] = 1;
} else if (distance === 1) {
// 中间层:白色
matrix[y + i][x + j] = 0;
} else {
// 中心:黑色
matrix[y + i][x + j] = 1;
}
}
}
}
}
}
/**
* 获取对齐图案位置
*/
function getAlignmentPatternPositions(version) {
// 二维码标准定义的对齐图案位置表
const alignmentPatterns = [
[], // 版本0未使用
[6, 18], // 版本1
[6, 22], // 版本2
[6, 26], // 版本3
[6, 30], // 版本4
[6, 34], // 版本5
[6, 22, 38], // 版本6
[6, 24, 42], // 版本7
// ... 其他版本省略
];
return alignmentPatterns[version] || [6, 18];
}2.3.3 数据填充:蛇形排列
特殊区域绘制完成后,就可以填充数据了。二维码的数据填充方式比较特别,是"蛇形"排列的:
从右下角开始,向上填充一列 然后向左移动一列,向下填充 再向左移动一列,向上填充 以此类推,直到所有数据都填充完毕
在填充过程中,需要跳过那些已经被特殊区域占用的位置。
/**
* 将数据填充到二维码矩阵
* @param {number[][]} matrix 初始化后的矩阵
* @param {number[]} codewords 交织后的码字数组
* @param {number} version 版本
* @returns {number[][]} 填充数据后的矩阵
*/
function fillDataToMatrix(matrix, codewords, version) {
const size = matrix.length;
let bitIndex = 0; // 当前处理的比特索引
let codewordIndex = 0; // 当前处理的码字索引
// 从右下角开始,按蛇形方向填充数据
// 列从右向左,从size-1到0(跳过定时图案列6)
for (let col = size - 1; col >= 0; col -= 2) {
// 处理偶数列(从下往上)和奇数列(从上往下)
// 注意:这里的奇偶是指列的遍历顺序,不是列索引的奇偶
// 先处理当前列(从下往上)
for (let row = size - 1; row >= 0; row--) {
// 跳过定时图案列
if (col === 6) continue;
// 填充当前模块(如果是待填充状态)
if (matrix[row][col] === -1) {
// 从当前码字中取一个比特
const bit = (codewords[codewordIndex] >> (7 - bitIndex)) & 1;
matrix[row][col] = bit;
bitIndex++;
// 如果当前码字的所有比特都已使用,移到下一个码字
if (bitIndex === 8) {
bitIndex = 0;
codewordIndex++;
// 如果所有码字都已使用,跳出循环
if (codewordIndex >= codewords.length) break;
}
}
}
// 如果所有码字都已使用,跳出循环
if (codewordIndex >= codewords.length) break;
// 处理左边一列(从上往下)
col--;
for (let row = 0; row < size; row++) {
// 跳过定时图案列
if (col === 6) continue;
// 填充当前模块(如果是待填充状态)
if (matrix[row][col] === -1) {
const bit = (codewords[codewordIndex] >> (7 - bitIndex)) & 1;
matrix[row][col] = bit;
bitIndex++;
if (bitIndex === 8) {
bitIndex = 0;
codewordIndex++;
if (codewordIndex >= codewords.length) break;
}
}
}
if (codewordIndex >= codewords.length) break;
}
return matrix;
}到这里,我们已经把所有数据都放到了矩阵的正确位置上。这个"蛇形"填充方式看起来有点反人类,但它是二维码标准规定的,咱们照着实现就好。
2.4 掩码优化:让二维码更好扫
现在我们已经有了一个完整的数据矩阵,但在最终生成图片前,还有一个重要步骤——掩码处理。
为什么需要掩码?因为原始数据矩阵可能会出现大片的相同颜色模块,或者形成某些不利于扫描识别的图案。掩码的作用就是通过特定的规则改变矩阵中某些模块的颜色(0变1,1变0),使得二维码更容易被扫描器识别。
2.4.1 8种掩码图案
二维码标准定义了8种掩码图案,每种图案都有一个对应的掩码函数:
掩码0:(i + j) % 2 === 0 掩码1:i % 2 === 0 掩码2:j % 3 === 0 掩码3:(i + j) % 3 === 0 掩码4:(Math.floor(i/2) + Math.floor(j/3)) % 2 === 0 掩码5:(ij) % 2 + (ij) % 3 === 0 掩码6:((ij) % 2 + (ij) % 3) % 2 === 0 掩码7:((i+j) % 2 + (i*j) % 3) % 2 === 0
我们需要为每种掩码定义一个函数:
/**
* 8种掩码函数
* @param {number} i 行索引
* @param {number} j 列索引
* @param {number} mask 掩码编号(0-7)
* @returns {boolean} 如果为true,则翻转该模块
*/
function maskFunctions(i, j, mask) {
switch (mask) {
case 0: return (i + j) % 2 === 0;
case 1: return i % 2 === 0;
case 2: return j % 3 === 0;
case 3: return (i + j) % 3 === 0;
case 4: return (Math.floor(i/2) + Math.floor(j/3)) % 2 === 0;
case 5: return ((i*j) % 2) + ((i*j) % 3) === 0;
case 6: return (((i*j) % 2) + ((i*j) % 3)) % 2 === 0;
case 7: return (((i + j) % 2) + ((i*j) % 3)) % 2 === 0;
default: return false;
}
}2.4.2 应用掩码
应用掩码很简单:遍历矩阵中的每个模块(特殊区域除外),如果掩码函数返回true,就翻转该模块的颜色(0变1,1变0)。
/**
* 应用掩码到矩阵
* @param {number[][]} matrix 数据矩阵
* @param {number} mask 掩码编号(0-7)
* @returns {number[][]} 应用掩码后的矩阵
*/
function applyMask(matrix, mask) {
const size = matrix.length;
// 创建矩阵副本,避免修改原矩阵
const maskedMatrix = matrix.map(row => [...row]);
for (let i = 0; i < size; i++) {
for (let j = 0; j < size; j++) {
// 只对数据区域应用掩码(特殊区域值为0或1,数据区域原始值为-1,但填充后为0或1)
// 这里简化处理,对所有非-1的模块应用掩码(实际应该排除格式信息和版本信息区域)
if (maskedMatrix[i][j] !== -1) {
if (maskFunctions(i, j, mask)) {
// 翻转模块颜色
maskedMatrix[i][j] = 1 - maskedMatrix[i][j];
}
}
}
}
return maskedMatrix;
}2.4.3 掩码评分:选择最佳掩码
有8种掩码,我们应该选哪一种呢?二维码标准定义了一套评分系统,通过计算每种掩码应用后的矩阵的"惩罚分数",分数越低的掩码效果越好。
评分规则有四条,都是为了避免出现不利于扫描的图案:
规则1:惩罚连续相同颜色的模块行或列(越长惩罚越高) 规则2:惩罚2x2的相同颜色方块 规则3:惩罚"黑白黑黑白"这样的特殊图案(可能被误识别为定位图案) 规则4:惩罚深色模块比例偏离50%的情况
/**
* 计算掩码的惩罚分数(越低越好)
* @param {number[][]} matrix 应用掩码后的矩阵
* @returns {number} 惩罚分数
*/
function calculatePenaltyScore(matrix) {
let score = 0;
const size = matrix.length;
// 规则1:连续相同颜色的模块
score += calculateRule1Penalty(matrix, size);
// 规则2:2x2相同颜色方块
score += calculateRule2Penalty(matrix, size);
// 规则3:特定图案(如黑白黑黑白)
score += calculateRule3Penalty(matrix, size);
// 规则4:深色模块比例
score += calculateRule4Penalty(matrix, size);
return score;
}
/**
* 规则1:连续相同颜色的模块
* 连续5个:1分,每多一个加1分
*/
function calculateRule1Penalty(matrix, size) {
let penalty = 0;
// 检查行
for (let i = 0; i < size; i++) {
let count = 1;
let prev = matrix[i][0];
for (let j = 1; j < size; j++) {
if (matrix[i][j] === prev) {
count++;
// 连续5个或更多
if (count >= 5) {
penalty++;
}
} else {
count = 1;
prev = matrix[i][j];
}
}
}
// 检查列
for (let j = 0; j < size; j++) {
let count = 1;
let prev = matrix[0][j];
for (let i = 1; i < size; i++) {
if (matrix[i][j] === prev) {
count++;
if (count >= 5) {
penalty++;
}
} else {
count = 1;
prev = matrix[i][j];
}
}
}
return penalty;
}
/**
* 规则2:2x2相同颜色方块
* 每个2x2方块罚25分
*/
function calculateRule2Penalty(matrix, size) {
let penalty = 0;
for (let i = 0; i < size - 1; i++) {
for (let j = 0; j < size - 1; j++) {
// 检查2x2方块的四个模块是否颜色相同
const val = matrix[i][j];
if (val === matrix[i][j+1] &&
val === matrix[i+1][j] &&
val === matrix[i+1][j+1]) {
penalty += 25;
}
}
}
return penalty;
}
/**
* 规则3:特定图案(如黑白黑黑白)
* 每个这样的图案罚40分
*/
function calculateRule3Penalty(matrix, size) {
let penalty = 0;
const patterns = [
[1,0,1,1,1,0,1,0,0,0,0], // 参考二维码规范定义的特定图案
[0,0,0,0,1,0,1,1,1,0,1]
];
// 检查所有可能的1x11或11x1区域
// 水平方向
for (let i = 0; i < size; i++) {
for (let j = 0; j <= size - 11; j++) {
// 提取11个连续模块
const window = [];
for (let k = 0; k < 11; k++) {
window.push(matrix[i][j + k]);
}
// 检查是否匹配任何一个模式
if (arraysEqual(window, patterns[0]) || arraysEqual(window, patterns[1])) {
penalty += 40;
}
}
}
// 垂直方向
for (let j = 0; j < size; j++) {
for (let i = 0; i <= size - 11; i++) {
// 提取11个连续模块
const window = [];
for (let k = 0; k < 11; k++) {
window.push(matrix[i + k][j]);
}
// 检查是否匹配任何一个模式
if (arraysEqual(window, patterns[0]) || arraysEqual(window, patterns[1])) {
penalty += 40;
}
}
}
return penalty;
}
/**
* 规则4:深色模块比例
* 比例每偏离50% 5%,罚10分
*/
function calculateRule4Penalty(matrix, size) {
// 计算深色模块总数
let darkCount = 0;
for (let i = 0; i < size; i++) {
for (let j = 0; j < size; j++) {
if (matrix[i][j] === 1) {
darkCount++;
}
}
}
// 计算比例
const totalModules = size * size;
const ratio = (darkCount / totalModules) * 100;
// 计算与50%的偏差,每5%偏差罚10分
const deviation = Math.abs(ratio - 50);
const penalty = Math.floor(deviation / 5) * 10;
return penalty;
}
// 辅助函数:判断两个数组是否相等
function arraysEqual(a, b) {
return a.length === b.length && a.every((val, index) => val === b[index]);
}2.4.4 选择最佳掩码
我们可以遍历所有8种掩码,计算每种掩码应用后的惩罚分数,然后选择分数最低的那个:
/**
* 选择最佳掩码并应用
* @param {number[][]} matrix 数据矩阵
* @returns {Object} { maskedMatrix: 应用最佳掩码后的矩阵, bestMask: 最佳掩码编号 }
*/
function selectAndApplyBestMask(matrix) {
let bestScore = Infinity;
let bestMask = 0;
let bestMatrix = null;
// 尝试所有8种掩码
for (let mask = 0; mask < 8; mask++) {
// 应用当前掩码
const maskedMatrix = applyMask(matrix, mask);
// 计算惩罚分数
const score = calculatePenaltyScore(maskedMatrix);
console.log(`掩码 ${mask} 得分: ${score}`);
// 更新最佳掩码
if (score < bestScore) {
bestScore = score;
bestMask = mask;
bestMatrix = maskedMatrix;
}
}
console.log(`选择最佳掩码: ${bestMask} (得分: ${bestScore})`);
return { maskedMatrix: bestMatrix, bestMask };
}掩码优化是提升二维码可读性的关键一步。一个好的掩码能让二维码的黑白模块分布更均匀,减少扫描器识别时的错误率。
2.5 格式信息与版本信息
最后,我们还需要在二维码中嵌入格式信息和版本信息(如果版本 >=7)。
2.5.1 格式信息嵌入
格式信息包含纠错级别和掩码编号,共15位数据,加上15位CRC校验码,总共30位。这些信息被放置在二维码的固定位置:
/**
* 嵌入格式信息
* @param {number[][]} matrix 二维码矩阵
* @param {string} errorCorrectionLevel 纠错级别('L', 'M', 'Q', 'H')
* @param {number} mask 掩码编号
*/
function embedFormatInformation(matrix, errorCorrectionLevel, mask) {
// 纠错级别编码
const ecLevelCodes = { 'L': 0b01, 'M': 0b00, 'Q': 0b11, 'H': 0b10 };
const ecCode = ecLevelCodes[errorCorrectionLevel];
// 格式信息数据:5位(纠错级别2位 + 掩码3位)
const formatData = (ecCode << 3) | mask;
// 计算15位CRC校验码(生成多项式:x^15 + x^10 + x^3 + 1)
const crc = calculateFormatInfoCRC(formatData);
// 组合成15位格式信息(数据5位 + CRC10位)
const formatInfo = (formatData << 10) | crc;
// 将格式信息转换为15位二进制字符串
let formatBinary = formatInfo.toString(2).padStart(15, '0');
// 格式信息位置:位于矩阵的两个地方(互为备份)
const positions = [
// 位置1:左上角定位图案旁边
[
{x: 8, y: 0}, {x: 8, y: 1}, {x: 8, y: 2}, {x: 8, y: 3}, {x: 8, y: 4}, {x: 8, y: 5}, {x: 8, y: 7}, {x: 8, y: 8},
{x: 7, y: 8}, {x: 5, y: 8}, {x: 4, y: 8}, {x: 3, y: 8}, {x: 2, y: 8}, {x: 1, y: 8}, {x: 0, y: 8}
],
// 位置2:右上角定位图案旁边
[
{x: size - 1, y: 8}, {x: size - 2, y: 8}, {x: size - 3, y: 8}, {x: size - 4, y: 8}, {x: size - 5, y: 8}, {x: size - 6, y: 8}, {x: size - 7, y: 8}, {x: size - 8, y: 8},
{x: size - 8, y: 7}, {x: size - 8, y: 5}, {x: size - 8, y: 4}, {x: size - 8, y: 3}, {x: size - 8, y: 2}, {x: size - 8, y: 1}, {x: size - 8, y: 0}
]
];
const size = matrix.length;
// 在两个位置嵌入格式信息
for (const posGroup of positions) {
for (let i = 0; i < posGroup.length; i++) {
const {x, y} = posGroup[i];
// 格式信息位(注意:这里需要根据二维码规范反转某些位)
const bit = parseInt(formatBinary[i], 2);
matrix[y][x] = bit;
}
}
return matrix;
}
/**
* 计算格式信息的CRC校验码
* @param {number} data 5位格式数据
* @returns {number} 10位CRC校验码
*/
function calculateFormatInfoCRC(data) {
// 生成多项式:x^10 + x^8 + x^5 + x^4 + x^2 + x^1 + 1 = 0x537
const poly = 0x537;
let crc = data << 10; // 左移10位,为CRC腾出空间
for (let i = 4; i >= 0; i--) { // 数据有5位
if ((crc >> (14 - i)) & 1) { // 如果当前位是1
crc ^= poly << (i);
}
}
return crc & 0x3FF; // 返回低10位
}2.5.2 版本信息嵌入(版本7及以上)
对于版本7及以上的二维码,还需要嵌入版本信息,共6位数据加上12位CRC校验码,总共18位:
/**
* 嵌入版本信息(版本7及以上)
* @param {number[][]} matrix 二维码矩阵
* @param {number} version 版本号
*/
function embedVersionInformation(matrix, version) {
if (version < 7) return matrix; // 版本7以下不需要版本信息
const size = matrix.length;
// 版本信息数据(6位)
const versionData = version;
// 计算12位CRC校验码(生成多项式:x^12 + x^11 + x^10 + x^9 + x^8 + x^5 + x^2 + 1)
const crc = calculateVersionInfoCRC(versionData);
// 组合成18位版本信息(数据6位 + CRC12位)
const versionInfo = (versionData << 12) | crc;
// 转换为18位二进制字符串
let versionBinary = versionInfo.toString(2).padStart(18, '0');
// 版本信息位置:右下角和左上角
const positions = [
// 右下角(6x3区域)
[
{x: size - 11, y: size - 9}, {x: size - 10, y: size - 9}, {x: size - 9, y: size - 9},
{x: size - 11, y: size - 10}, {x: size - 10, y: size - 10}, {x: size - 9, y: size - 10},
{x: size - 11, y: size - 11}, {x: size - 10, y: size - 11}, {x: size - 9, y: size - 11},
{x: size - 11, y: size - 12}, {x: size - 10, y: size - 12}, {x: size - 9, y: size - 12},
{x: size - 11, y: size - 13}, {x: size - 10, y: size - 13}, {x: size - 9, y: size - 13},
{x: size - 11, y: size - 14}, {x: size - 10, y: size - 14}, {x: size - 9, y: size - 14}
],
// 左上角(6x3区域),与右下角对称
[
{x: 8, y: size - 11}, {x: 8, y: size - 10}, {x: 8, y: size - 9},
{x: 7, y: size - 11}, {x: 7, y: size - 10}, {x: 7, y: size - 9},
{x: 6, y: size - 11}, {x: 6, y: size - 10}, {x: 6, y: size - 9},
{x: 5, y: size - 11}, {x: 5, y: size - 10}, {x: 5, y: size - 9},
{x: 4, y: size - 11}, {x: 4, y: size - 10}, {x: 4, y: size - 9},
{x: 3, y: size - 11}, {x: 3, y: size - 10}, {x: 3, y: size - 9}
]
];
// 在两个位置嵌入版本信息
for (const posGroup of positions) {
for (let i = 0; i < posGroup.length; i++) {
const {x, y} = posGroup[i];
const bit = parseInt(versionBinary[i], 2);
matrix[y][x] = bit;
}
}
return matrix;
}
/**
* 计算版本信息的CRC校验码
* @param {number} data 6位版本数据
* @returns {number} 12位CRC校验码
*/
function calculateVersionInfoCRC(data) {
// 生成多项式:x^12 + x^11 + x^10 + x^9 + x^8 + x^5 + x^2 + 1 = 0x1F25
const poly = 0x1F25;
let crc = data << 12; // 左移12位,为CRC腾出空间
for (let i = 5; i >= 0; i--) { // 数据有6位
if ((crc >> (17 - i)) & 1) { // 如果当前位是1
crc ^= poly << (i);
}
}
return crc & 0xFFF; // 返回低12位
}2.6 二维码绘制:从矩阵到图像
终于到了最后一步:把我们构建的矩阵绘制到屏幕上。我们可以用HTML5 Canvas来实现:
/**
* 在Canvas上绘制二维码
* @param {number[][]} matrix 二维码矩阵
* @param {HTMLElement} canvasElement Canvas元素
* @param {number} moduleSize 每个模块的像素大小
* @param {number} margin 边距(模块数)
*/
function drawQRCodeOnCanvas(matrix, canvasElement, moduleSize = 5, margin = 4) {
const size = matrix.length;
const canvasSize = size * moduleSize + margin * 2 * moduleSize;
// 设置Canvas大小
canvasElement.width = canvasSize;
canvasElement.height = canvasSize;
const ctx = canvasElement.getContext('2d');
// 填充背景(白色)
ctx.fillStyle = '#FFFFFF';
ctx.fillRect(0, 0, canvasSize, canvasSize);
// 设置模块颜色(黑色)
ctx.fillStyle = '#000000';
// 绘制二维码模块
for (let y = 0; y < size; y++) {
for (let x = 0; x < size; x++) {
// 如果是黑色模块
if (matrix[y][x] === 1) {
const drawX = margin * moduleSize + x * moduleSize;
const drawY = margin * moduleSize + y * moduleSize;
ctx.fillRect(drawX, drawY, moduleSize, moduleSize);
}
}
}
}三、完整流程整合与实战演示
现在我们已经实现了所有核心功能,让我们把它们整合起来,打造一个完整的二维码生成器:
/**
* 二维码生成器主函数
* @param {string} text 要编码的文本
* @param {Object} options 配置选项
* @returns {number[][]} 生成的二维码矩阵
*/
function generateQRCode(text, options = {}) {
// 默认配置
const config = {
version: options.version || 1, // 版本(1-40)
errorCorrectionLevel: options.errorCorrectionLevel || 'L', // 纠错级别('L', 'M', 'Q', 'H')
mask: options.mask, // 掩码(0-7),不指定则自动选择
...options
};
console.log('开始生成二维码:', config);
// 1. 数据编码
const encodedDataBits = encodeData(text, config.version);
console.log('数据编码完成,长度:', encodedDataBits.length);
// 2. 纠错码生成与交织
const codewords = processErrorCorrection(encodedDataBits, config.version, config.errorCorrectionLevel);
console.log('纠错码生成完成,码字数量:', codewords.length);
// 3. 创建矩阵并绘制固定图案
let matrix = createQRMatrix(config.version);
console.log('矩阵初始化完成,大小:', matrix.length, 'x', matrix[0].length);
// 4. 填充数据
matrix = fillDataToMatrix(matrix, codewords, config.version);
console.log('数据填充完成');
// 5. 应用掩码(自动选择或使用指定掩码)
let maskedResult;
if (config.mask !== undefined && config.mask >= 0 && config.mask <= 7) {
// 使用指定掩码
maskedResult = {
maskedMatrix: applyMask(matrix, config.mask),
bestMask: config.mask
};
} else {
// 自动选择最佳掩码
maskedResult = selectAndApplyBestMask(matrix);
}
console.log('掩码应用完成,使用掩码:', maskedResult.bestMask);
// 6. 嵌入格式信息
matrix = embedFormatInformation(
maskedResult.maskedMatrix,
config.errorCorrectionLevel,
maskedResult.bestMask
);
// 7. 嵌入版本信息(如果需要)
matrix = embedVersionInformation(matrix, config.version);
console.log('二维码生成完成!');
return matrix;
}3.1 完整使用示例
现在,让我们用一个完整的HTML页面来演示如何使用我们的二维码生成器:
<!DOCTYPE html>
<html>
<head>
<title>手撸二维码生成器</title>
<style>
body { font-family: Arial, sans-serif; max-width: 800px; margin: 0 auto; padding: 20px; }
.container { display: flex; flex-direction: column; gap: 20px; }
.input-group { display: flex; gap: 10px; }
#textInput { flex: 1; padding: 10px; font-size: 16px; }
#generateBtn { padding: 10px 20px; background: #007bff; color: white; border: none; border-radius: 4px; cursor: pointer; }
#generateBtn:hover { background: #0056b3; }
.options { display: flex; gap: 15px; margin-top: 10px; }
.option-group { display: flex; flex-direction: column; }
canvas { border: 1px solid #ddd; margin: 0 auto; }
.info { margin-top: 20px; padding: 15px; background: #f5f5f5; border-radius: 4px; }
</style>
</head>
<body>
<div class="container">
<h1>手撸二维码生成器</h1>
<div class="input-group">
<input type="text" id="textInput" placeholder="输入要编码的文本..." value="https://example.com">
<button id="generateBtn">生成二维码</button>
</div>
<div class="options">
<div class="option-group">
<label>纠错级别:</label>
<select id="ecLevelSelect">
<option value="L">低 (7%)</option>
<option value="M" selected>中 (15%)</option>
<option value="Q">较高 (25%)</option>
<option value="H">高 (30%)</option>
</select>
</div>
<div class="option-group">
<label>版本:</label>
<select id="versionSelect">
<option value="1" selected>1 (21x21)</option>
<option value="2">2 (25x25)</option>
<option value="3">3 (29x29)</option>
<option value="4">4 (33x33)</option>
<option value="5">5 (37x37)</option>
</select>
</div>
<div class="option-group">
<label>模块大小:</label>
<input type="number" id="moduleSizeInput" value="5" min="1" max="20">
</div>
</div>
<canvas id="qrcodeCanvas"></canvas>
<div class="info">
<h3>二维码信息</h3>
<div id="qrcodeInfo">等待生成...</div>
</div>
</div>
<script>
// 这里放置前面实现的所有函数...
// 页面交互逻辑
document.addEventListener('DOMContentLoaded', () => {
const textInput = document.getElementById('textInput');
const generateBtn = document.getElementById('generateBtn');
const ecLevelSelect = document.getElementById('ecLevelSelect');
const versionSelect = document.getElementById('versionSelect');
const moduleSizeInput = document.getElementById('moduleSizeInput');
const qrcodeCanvas = document.getElementById('qrcodeCanvas');
const qrcodeInfo = document.getElementById('qrcodeInfo');
// 生成二维码按钮点击事件
generateBtn.addEventListener('click', generateAndDisplayQRCode);
// 初始生成一次二维码
generateAndDisplayQRCode();
function generateAndDisplayQRCode() {
const text = textInput.value.trim();
if (!text) {
alert('请输入要编码的文本');
return;
}
try {
const version = parseInt(versionSelect.value);
const errorCorrectionLevel = ecLevelSelect.value;
const moduleSize = parseInt(moduleSizeInput.value);
// 记录开始时间
const startTime = performance.now();
// 生成二维码矩阵
const qrMatrix = generateQRCode(text, {
version,
errorCorrectionLevel
});
// 计算生成时间
const generateTime = (performance.now() - startTime).toFixed(2);
// 绘制二维码
drawQRCodeOnCanvas(qrMatrix, qrcodeCanvas, moduleSize);
// 更新信息面板
qrcodeInfo.innerHTML = `
<p>文本: ${text}</p>
<p>版本: ${version} (${qrMatrix.length}x${qrMatrix[0].length} 模块)</p>
<p>纠错级别: ${errorCorrectionLevel} (${
{ 'L': '7%', 'M': '15%', 'Q': '25%', 'H': '30%' }[errorCorrectionLevel]
} 纠错能力)</p>
<p>生成时间: ${generateTime}ms</p>
`;
} catch (error) {
console.error('生成二维码失败:', error);
alert('生成二维码失败: ' + error.message);
}
}
});
</script>
</body>
</html>四、性能优化与高级特性
4.1 性能优化技巧
我们的基础实现虽然功能完整,但性能上还有优化空间,尤其是在处理高版本二维码时:
预计算查找表:伽罗瓦域乘法表、生成多项式等可以预先计算并缓存,避免重复计算 矩阵操作优化:使用TypedArray代替普通数组存储矩阵,提高内存效率和访问速度 分块并行处理:在支持Web Worker的环境中,可以将分块编码和纠错码计算并行处理 算法优化:某些循环可以使用位运算代替算术运算,提高执行效率
下面是伽罗瓦域乘法表的预计算优化示例:
// 预计算GF(2^8)乘法表和指数表(只计算一次)
const GF_TABLES = (function() {
const mulTable = new Uint8Array(256 * 256);
const logTable = new Uint8Array(256);
const expTable = new Uint8Array(512); // 扩展到512以避免模运算
// 不可约多项式: x⁸ + x⁴ + x³ + x² + 1 = 0x11D
const irreducible = 0x11D;
// 生成指数表和对数表(α=2)
let x = 1;
for (let i = 0; i < 255; i++) {
expTable[i] = x;
logTable[x] = i;
x <<= 1; // 乘以2
if (x & 0x100) { // 如果超过8位
x ^= irreducible; // 模不可约多项式
}
}
// 填充剩余的指数表(循环)
for (let i = 255; i < 512; i++) {
expTable[i] = expTable[i % 255];
}
// 生成乘法表
for (let a = 0; a < 256; a++) {
for (let b = 0; b < 256; b++) {
if (a === 0 || b === 0) {
mulTable[a * 256 + b] = 0;
} else {
const logA = logTable[a];
const logB = logTable[b];
mulTable[a * 256 + b] = expTable[logA + logB];
}
}
}
return {
mul: (a, b) => mulTable[a * 256 + b],
log: (x) => logTable[x],
exp: (e) => expTable[e]
};
})();
// 使用优化后的伽罗瓦域乘法
function gfMultiplyOptimized(a, b) {
return GF_TABLES.mul(a, b);
}4.2 高级特性实现
基于我们的基础实现,还可以添加一些高级特性:
自定义颜色:支持自定义二维码的前景色和背景色 Logo嵌入:在二维码中心嵌入Logo(注意:会降低纠错能力) 二维码美化:支持圆角模块、渐变颜色等美化效果 支持不同输出格式:除了Canvas,还支持SVG、PNG图片输出
下面是一个支持Logo嵌入的实现示例:
/**
* 在二维码上嵌入Logo
* @param {HTMLCanvasElement} canvas Canvas元素
* @param {string} logoUrl Logo图片URL
* @param {number} logoSizeRatio Logo大小比例(0-1)
*/
function embedLogo(canvas, logoUrl, logoSizeRatio = 0.2) {
return new Promise((resolve, reject) => {
const ctx = canvas.getContext('2d');
const logoImg = new Image();
logoImg.crossOrigin = 'anonymous'; // 处理跨域图片
logoImg.onload = () => {
const canvasSize = canvas.width;
const logoSize = canvasSize * logoSizeRatio;
const logoX = (canvasSize - logoSize) / 2;
const logoY = (canvasSize - logoSize) / 2;
// 绘制白色背景圆圈(可选)
ctx.beginPath();
ctx.arc(canvasSize/2, canvasSize/2, logoSize/2 + canvasSize * 0.02, 0, Math.PI * 2);
ctx.fillStyle = '#ffffff';
ctx.fill();
// 绘制Logo
ctx.drawImage(logoImg, logoX, logoY, logoSize, logoSize);
// 添加白色边框(可选)
ctx.beginPath();
ctx.arc(canvasSize/2, canvasSize/2, logoSize/2, 0, Math.PI * 2);
ctx.lineWidth = canvasSize * 0.01;
ctx.strokeStyle = '#ffffff';
ctx.stroke();
resolve();
};
logoImg.onerror = () => reject(new Error('无法加载Logo图片'));
logoImg.src = logoUrl;
});
}4.3 常见问题与解决方案
在实现二维码生成器的过程中,可能会遇到一些常见问题:
生成的二维码无法扫描
检查数据编码是否正确,特别是模式指示器和字符计数 验证纠错码生成是否正确,重点检查Reed-Solomon实现 确认矩阵填充方向是否正确(蛇形填充) 检查掩码是否正确应用
中文或特殊字符编码问题
确保字节模式使用UTF-8编码 对于汉字模式,需使用GB2312编码(注意:并非所有扫描器都支持)
性能问题
预计算查找表(伽罗瓦域乘法表、生成多项式等) 避免频繁创建大型数组,使用对象池或复用数组 对高版本二维码使用Web Worker进行后台处理
五、前端工程师的二维码技术图谱
通过实现这个二维码生成器,我们接触到了多个领域的知识和技术:
5.1 核心技术栈

5.2 延伸学习路径
如果你对二维码技术感兴趣,可以进一步学习以下相关技术:
条码技术:Code 128、EAN-13等其他条码的编码原理 高级纠错码:LDPC码、Turbo码等现代纠错编码技术 图像处理:二维码识别算法(边缘检测、畸变校正等) 增强现实:基于二维码的AR应用开发 加密技术:结合加密算法实现安全二维码
六、总结与展望
亲爱的前端工友们,到这里我们已经一起从0到1实现了一个完整的二维码生成器。回顾整个过程,我们从数据编码开始,深入理解了Reed-Solomon纠错码的数学原理,学习了二维码矩阵的构造方法,最后通过Canvas将矩阵绘制为图像。
这个过程虽然充满了挑战(尤其是伽罗瓦域运算和Reed-Solomon编码部分),但也让我们深刻体会到了一个看似简单的二维码背后所蕴含的精妙设计和深厚技术积累。
6.1 关键技术点回顾
数据编码:根据内容自动选择最优编码模式,提高数据密度 纠错编码:使用Reed-Solomon码实现强大的错误恢复能力 矩阵构造:精确放置各种功能图案,确保二维码可识别 掩码优化:通过科学的评分系统选择最佳掩码,提高扫描成功率 图形绘制:将数据矩阵转换为视觉图像
6.2 实际应用建议
在实际项目中,如果需要使用二维码功能,我建议:
优先使用成熟库:如qrcode.js、zxing等,这些库经过了充分测试和优化 理解原理再定制:如果需要定制功能,先深入理解二维码标准和编码原理 注意性能优化:对于大量或高版本二维码生成,考虑使用Web Worker或服务端生成 测试多种扫描器:不同扫描器对二维码的识别能力有差异,需多设备测试
6.3 技术探索无止境
二维码技术虽然已经非常成熟,但仍有创新空间:
彩色二维码:通过多颜色提高数据密度 动态二维码:结合动画效果的动态二维码 三维二维码:在3D空间中实现的二维码 隐形二维码:肉眼不可见但扫描器可识别的二维码
作为前端工程师,我们不仅要会使用工具,更要理解工具背后的原理。这种"知其然,也知其所以然"的精神,正是推动我们不断进步的动力。
希望这篇文章能让你对二维码技术有更深入的理解,也希望它能激发你探索更多底层技术的兴趣。
附录:参考资料
QR Code Tutorial - 最权威的二维码技术教程 ISO/IEC 18004 - 二维码国际标准 Reed-Solomon Codes - 里德-所罗门码维基百科 GF(2^8) Arithmetic - 伽罗瓦域运算详解 QR Code Generator - 优秀的二维码生成库源码 二维码生成